Latihan Soal Sifat - Sifat Gradien Pada Persamaan Garis Lurus Matematika Kelas 8 Kurikulum 2013 dan Pembahasannya

Latihan Soal Sifat - Sifat Gradien Pada Persamaan Garis Lurus Matematika Kelas 8 Kurikulum 2013 dan Pembahasannya ini terdiri dari soal tentang sifat gradien. Gradien adalah tingkat kemiringan suatu garis, yang disimbolkan dengan m.

Sifat - Sifat Gradien :

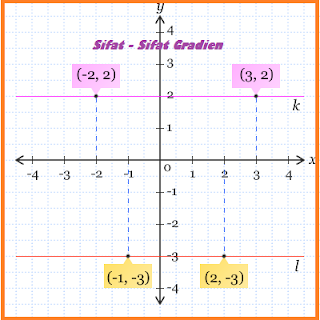
1. Gradien garis yang sejajar dengan sumbu-x, m = 0
2. Garis yang sejajar dengan sumbu-y tidak memilki gradien
3. Gradien dua garis yang sejajar adalah sama, m1 = m2
4. Gradien dua garis yang tegak lurus, m1 x m2 = -1

Berikut ini beberapa contoh Latihan Soal Gradien pada Persamaan Garis Lurus Kelas 8 Kurikulum 2013 dan Pembahasannya:

Tentukan apakah kedua garis tersebut sejajar atau tegak lurus?

a. Garis k yang melalui titik A(7, -3) dan B(11, 3)

    Garis l yang melalui titik C(-9, 0) dan D(-5, 6)

b. Garis m yang melalui titik P(3, 5) dan Q(0,0)

    Garis n yang melalui titik R(0, 0) dan S(-5, 3)

Pembahasan:

a. Mencari gradien garis k

Untuk titik A(7, -3), maka x1 = 7 dan y1= -3

Untuk titik B(11, 3), maka x2 = 11 dan y2 = 3.

mAB = y2 -  y1

           x2 - x1

mAB = 3 - (-3)

          11 - 7

mAB = 3+3/4

mAB = 6/4

Mencari gradien garis l

Untuk titik C(-9, 0), maka x1 = -9 dan y1= 0

Untuk titik D(-5, 6), maka x2 = -5 dan y2 = 6.

mCD = y2 -  y1

           x2 - x1

mCD =   6 - 0

          -5 - (-9)

mCD = 6/-5+9

mCD = 6/4

Karena mAB = mCD = 6/4, maka garis k dan l sejajar.

b. Mencari gradien garis m

Untuk titik P(3, 5), maka x1 = 3 dan y1= 5

Untuk titik Q(0,0), maka x2 = 0 dan y2 = 0.

mPQ = y2 -  y1

           x2 - x1

mPQ = 0 - 5

          0 - 3

mPQ = -5/-3 = 5/3

Mencari gradien garis n

Untuk titik R(0, 0), maka x1 = 0 dan y1= 0

Untuk titik S(-5, 3), maka x2 = -5 dan y2 = 3.

mRS = y2 -  y1

           x2 - x1

mRS = 3 - 0

         -5 - 0

mRS = 3/-5

Karena mPQ x mRS = -1

              5/3 x  3/-5 = -1, maka garis m dan n saling tegak lurus.

Untuk lebih lengkapnya, silakan klik tautan berikut:
Soal Ulangan Harian Persamaan Garis Lurus Kelas 8 Kurikulum 2013 dan Pembahasannya

File yang kami upload semuanya tersimpan di Google Drive dengan demikian akan sangat terjamin keamanannya, terhindar dari infeksi virus seperti malware dan adware. Software Pendukung: Microsoft Excel [xlsx] | Microsoft Word [docx] | [pdf] Sosmed : Facebook | Google Plus | Twitter

Diharapkan dengan Latihan Soal Sifat - Sifat Gradien Pada Persamaan Garis Lurus Matematika Kelas 8 Kurikulum 2013 dan Pembahasannya ini dapat bermanfaat baik Guru maupun Siswa dalam mempersiapkan diri menjelang kegiatan Ulangan dan Ujian khususnya untuk Mata Pelajaran matematika. Kritik dan saran saya harapkan untuk kemajuan blog ini dimasa yang akan datang. Dapatkan berbagai Soal UH, UTS, UAS, UKK, UN, TO yang saya sediakan secara gratis dalam blog ini.