Soal Ulangan Harian Persamaan Kuadrat Matematika Kelas X SMA Kurikulum 2013 dan Pembahasannya - ini akan kami bagikan dimana pada postingan sebelumnya telah kami bagikan Soal Ulangan Harian Barisan dan Deret Matematika Kelas X Kurikulum 2013. Persamaan kuadrat dalam x mempunyai bentuk umum: ax2 + bx + c = 0 , a ¹ 0 a, b dan c adalah bilangan real.
- Menyelesaikan Persamaan Kuadrat dengan Memfaktorkan (Faktorisasi)
Nilai x1 dan x2 disebut akar-akar (penyelesaian) persamaan kuadrat.
- Menyelesaikan Persamaan Kuadrat dengan Melengkapkan Kuadrat Sempurna
Persamaan kuadrat ax2 + bx + c = 0 dapat diselesaikan dengan mengubahnya menjadi (x + p)2 = q.
- Menyelesaikan Persamaan Kuadrat dengan Menggunakan Rumus Kuadratis (Rumus ABC)
Persamaan kuadrat ax2 + bx + c = 0 dapat diselesaikan dengan menggunakan rumus berikut:
Berikut ini contoh Soal Ulangan Harian Persamaan Kuadrat Matematika Kelas X SMA Kurikulum 2013 dan Pembahasannya:
Soal No.1: Selesaikan x2 – 4 x + 3 = 0
Pembahasan:
x2 – 4 x + 3 = 0
(x – 3) (x – 1) = 0
x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1
Jadi, penyelesaian dari x2 – 4 x + 3 = 0 adalah { 3 , 1}
Soal No.2: Tentukan himpunan penyelesaian dari x2 – 6 x + 5 = 0.
Pembahasan:
x2 – 4 x + 3 = 0
(x – 3) (x – 1) = 0
x – 3 = 0 atau x – 1 = 0
x = 3 atau x = 1
Jadi, penyelesaian dari x2 – 4 x + 3 = 0 adalah { 3 , 1}
Soal No.2: Tentukan himpunan penyelesaian dari x2 – 6 x + 5 = 0.
Pembahasan:
x2 – 6 x + 5 = 0
x2 – 6 x + 9 – 4 = 0
x2 – 6 x + 9 = 4
(x – 3)2 = 4
x – 3 = 2 atau x – 3 = –2
x = 5 atau x = 1
Jadi, himpunan penyelesaiannya adalah{ 1 , 5}.
Soal No.3: Jika akar-akar persamaan x2 - 3x - 10 = 0 adalah x1 dan x2, maka hasil dari x1 + x2 sama dengan ....
A. x1 + x2 = 3
B. x1 + x2 = 4
C. x1 + x2 = 5
D. x1 + x2 = 7
Pembahasan :
Dengan metode pemfaktoran :
⇒ x2 - 3x - 10 = 0
⇒ (x + 2)(x - 5) = 0
⇒ x1 = -2 atau x2 = 5
Jumlah akar-akarnya adalah:
⇒ x1 + x2 = -2 + 5
⇒ x1 + x2 = 3
Cara cepat:
Dari x2 - 3x - 10 = 0
Dik : a = 1, b = -3, c = -10
Jumlah akar:
⇒ x1 + x2 = -b/a
⇒ x1 + x2 = -(-3)/1
⇒ x1 + x2 = 3
Untuk lebih lengkapnya, silakan klik tautan berikut:
Download Soal Ulangan Harian Persamaan Kuadrat Matematika Kelas X SMA Kurikulum 2013 dan Pembahasannya
Diharapkan dengan Soal Ulangan Harian Persamaan Kuadrat Matematika Kelas X SMA Kurikulum 2013 dan Pembahasannya ini dapat bermanfaat baik Guru maupun Siswa dalam mempersiapkan diri menjelang kegiatan Ulangan dan Ujian khususnya untuk Mata Pelajaran matematika. Kritik dan saran saya harapkan untuk kemajuan blog ini dimasa yang akan datang. Dapatkan berbagai Soal UH, UTS, UAS, UKK, UN, TO yang saya sediakan secara gratis dalam blog ini.


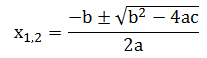
Posting Komentar